I/O OVER

Haskell 学习笔记 (二)

Train Train ·

这次是 type class 到 monad 的初步。初学者的读书笔记而已

Kind

类型构造器 (type constructor) 或许可以当成类型上的“函数”。在类型上 [Int] 其实是 [] Int 的语法糖，两者是等价的，[] 是类型构造器，可以看作类似函数的东西，而将参数 Int 应用于 [] 最后就会得到 [Int]。 可以用 kind 描述它的“函数签名”。Int Int -> Bool [Int] -> [[Bool]] 它们的 kind 就是 *，意味着整个类型都被确定了下来，没有可以变动的地方。而 Maybe 或者 [] 这种，需要一个普通的 a :: * 来补全，才能获得最终的类型（如Maybe Bool , [Int]），这样的类型构造器的类型就是 * -> *。

当然也可以有 * -> * -> * 乃至更多，无非是需要更多类型参数来补全而已。比如说 Either :: * -> * -> *。

像函数一样也可以把类型偏应用到构造器上，获得一个新的构造器。

> :k Either Int
Either Int :: * -> *

函数箭头其实也是一个类型构造器，左侧有一个类型，右侧有一个类型，最终构造一个函数类型 (->) :: * -> * -> *。所以 curry 化就是箭头的直接效果……吧？

注意类型构造器别和数据构造器 (data constructor) 搞混了，Maybe 是类型构造器而 Just 是数据构造器，实际上算是一种普通函数。

高阶的 kind

普通语言要么没有泛型，只能定义普通的类型，要么有：

struct Foobar<A, B> {
    foo: A,
    bar: B,
}

其中 A 和 B 是两个需要给定的类型，并且它们的 kind 只能是 *，也就说不带泛型参数、或者参数全被填满的普通类型，用 kind 来表示就是 Foobar :: * -> * -> *。

没办法做到1：

struct Foobar<A, B> {
    foobar: A<B>
}

（C++ 模版是例外……）

也就是说假如有列表容器 List<T>，我们可以有 Foobar<List, Int>，foobar 字段的类型就会是 List<Int>。这样做的意义在于我们可以更换容器，随意把 List 换成 Array 或者 Linked List。

编译器要限定 A 为一个 kind 为 * -> * 的类型构造器，而整个 Foobar 的 kind 就为 Foobar ::(* -> *) -> * -> * 。

有了括号。联想一下高阶函数的类型：(a -> b) -> c 。

Haskell 可以定义：

newtype Foobar f a = Foobar (f a)

然后就：

> Foobar (42::Int)

-- 一堆错误信息。 Haskell 的错误信息好难懂啊……

> :t Foobar $ Just (42::Int)
Foobar $ Just (42::Int) :: Foobar Maybe Int

空白的值出错了，而对于 Maybe 值成功地返回了一个 Foobar Maybe Int 类型。

Type class

Type class (类型类) 类似于别的语言中的 Interface (接口) 或者 Trait (特质)。用来抽象出不同类型中相似的操作。

比如说可以规定某种类型之间可以判断是否相等：

data Foobar = Foo | Bar

instance Eq Foobar where
  Foo == Foo = True
  Bar == Bar = True
  _   == _   = False

Type class 也能：

instance (Foo a) => Bar a where
   bar = foo

这里的意思是，对所有属于 Foo 的类型实现 Bar，a 这个被约束到了 Foo。

Type class 不仅仅能为 a :: * 的类型实现，还能对类型构造器来实现。

Functor

Functor (函子)，只能实现于 t :: * -> * 的类型构造器。这就是对类型构造器实现 type class 的例子。

class Functor f where
  fmap :: (a -> b) -> f a -> f b

使之满足 fmap id = id，以及分配律：

fmap (f.g) = fmap f . fmap g

Haskell 不能自己验证，需要程序员保证。

对 [] 类型来说，fmap 就是 map。

虽然一般用于容器上，但其实并不是只能用于容器的，只要满足规则的东西都能是函子。

函数箭头其实也是个类型构造器 (->) :: * -> * -> *，对其偏应用一个多态类型 r 后 ((->) r) :: * -> * ，这也是函子，fmap 就是函数复合 .：

instance Functor ((->) r) where
  fmap = (.)


fmap :: (a -> b) -> f a -> f b
fmap :: (a -> b) -> ((->) r) a -> ((->) r) b  -- f 代换为 ((->) r)
(.) :: (a -> b) -> (r -> a) -> r -> b

以前的文章版本遗留下来的一幅图：

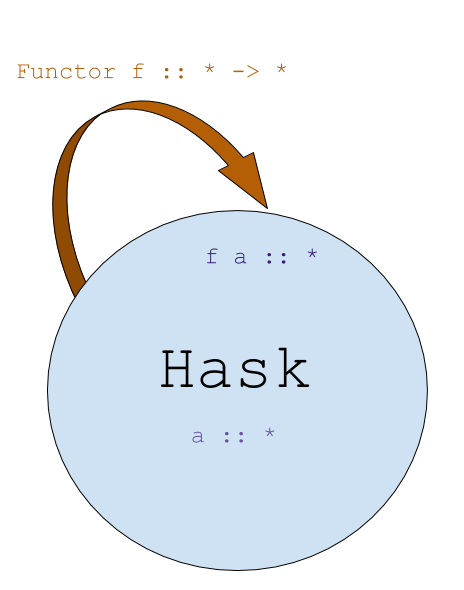
functor

Monad

class Monad m where
  (>>=) :: m a -> (a -> m b) -> m b -- 称 bind
  return :: a -> m a

需要实现者保证满足：

return x >>= f = f x -- 左单位元
m >>= return = m -- 右单位元
(m >>= f) >>= g = m >>= (\x -> f x >>= g) -- 结合律

也就是说，一个 Monad 需要实现两种操作，满足三种性质，只要这样就是 monad 了。

讲完了，已经理解了！两分钟理解 Monad！2

什么副作用啊，什么模拟序列操作呀，什么 CPS 呀……都是 Monad 的外延而不是内涵。

推荐看知乎上的这个回答。

参考的资料

  1. 以前我不懂这些，发现用 Rust 定义不出 Monad，还跑去发帖问了 orz。 ↩

  2. 这里有一篇文章图解，还有多看点实际的程序，书上很不错的内容我就不抄下来了。 ↩